<< Előző oldal    Következő oldal >>

 

Robert May ökológiai szimulációja

Az ökológia az élőlények és környezetük viszonyával, kölcsönhatásával foglalkozik. Jellemzően ökológiai feladat egy adott faj népességváltozásának vizsgálata egy adott környezetben. Például egy tóba betelepített halfaj egyedszámának alakulása. Az ökológusok matematikai modellekkel írják le az efféle folyamatokat, amelyek segítségével előre kiszámítható a népesség alakulása, akár több évre vagy évtizedre is.

A matematikus és biológus Robert May körültekintően megvizsgálta az alábbi egyszerű ökológiában használt képletet, és különös dolgot tapasztalt.

ahol x _előző jelenti az előző időszakban meglévő egyedek számát; x _következő a következő időszakban létező egyedek számát; r pedig a növekedési ráta. (A képlet biológiai értelmezésével részletesebben nem foglalkozunk.)

May különböző kezdőértékekkel és növekedési rátákkal vizsgálta az egyenlet viselkedését. Ezt mi magunk is megtehetjük a következő programmal. (Lista) Vizsgáljunk meg néhány értékpárt! Milyen lefolyású az összefüggés az x _kezdő = 0,4 és r = 2,8 feltételek esetén?

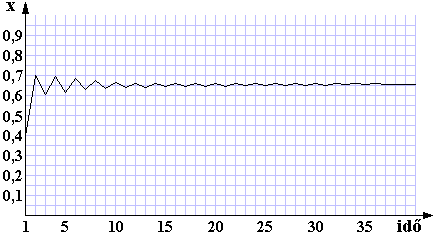
Láthatjuk, hogy az egyenlet segítségével számított sorozatunk egy meghatározott értékhez (0,655172…) tart. Tehát úgy viselkedik, ahogy változatlan körülmények között egy faj népességének változása általában lezajlik. A népesség állandósul.

Növeljük r értékét! (x _kezdő = 0,4; r = 3,2)

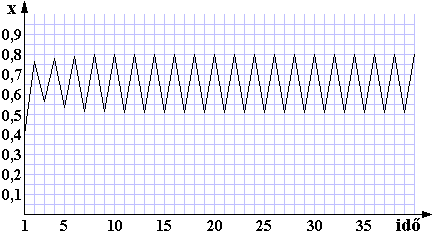
Különös dolgot tapasztalunk, a sorozat két érték (0,799455… és 0,513044…) között váltakozik. Növeljük tovább r-t! (x _kezdő = 0,4; r = 3,5)

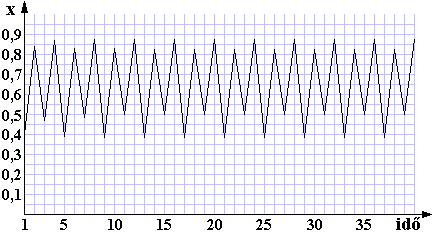
Ha megvizsgáljuk a grafikont, láthatjuk, hogy x négy azonos érték között váltakozik egy meghatározott sorrend szerint (0,874997…; 0,382819…; 0,826940…; 0,500884…). Végül próbáljuk ki az x _kezdő = 0,4 és r = 3,7 értékpárt!

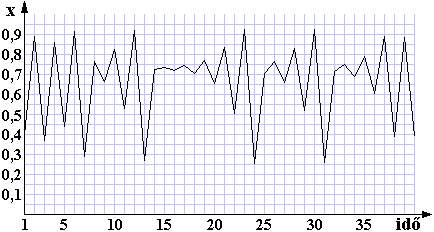
A grafikonunknál sokkal hosszabb időtartamban vizsgálva sem tapasztalunk ismétlődési periódust, habár a görbe hasonló jellegű szakaszokból áll. Megfigyelhetjük, hogy a meredekség nem vált minden lépésben előjelet; például a 13., 14. és 15. pontok között folyamatosan emelkedik.

Robert May – tapasztalva, hogy ez az egyszerű összefüggés milyen bonyolult számítási eredményeket produkálhat – alaposabb vizsgálatokat végzett. Különféle kezdőértékek esetén nagyon kis lépésekben futatta végig az r értékét és ábrázolta az így kapott állandósult x értékeket r függvényében. Ezt láthatjuk az alábbi ábrán az x _kezdő = 0,4 kezdőértékkel.

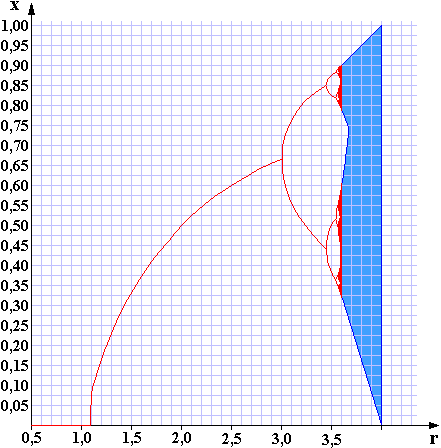
Az r = 0..1,1 tartományban az összefüggés nullához tart, ami az ökológiában a faj kihalását jelenti.

Az r = 1,1..3 tartományban az összefüggés egy 0 és 0,667 közötti számhoz tart. A számítás során megfigyelhetjük, hogy minél közelebb vagyunk az r = 3 értékhez, annál nehezebben áll be az ábrán jelölt érték. Az r = 3 értéknél az összefüggésünk több, mint 50 000 lengés után közelíti csak meg a 2/3 értéket (,amihez tart) három tizedesjegynyi pontossággal. Ez r = 1,5 esetén már három lengés után megtörténik. Ezek a lengések láthatók az oldal első ábráján r = 2,8 esetére.

Az r = 3 érték után a grafikon kettéválik, amely megfelel az oldal második ábrájának. Az összefüggés számított értéke két szám között váltakozik periodikusan.

És körülbelül az r = 3,45 értéknél a grafikon mindkét ága újra szétágazik, és így már négy számot ad meg, amelyeket az összefüggésünk szintén periodikusan felváltva vesz fel. Ezután minden ág újra elágazik, majd ismét, és ismét… És az r értékét mindig egyre kevesebbel kell növelnünk ahhoz, hogy újabb elágazásokhoz jussunk. Ennek következménye az, hogy az r = 3,5 érték után a grafikon besűrűsödik és az r = 3,6 értéknél már véletlenszerűnek tűnő eredményeket kapunk, amelyek azért egy meghatározott tartományban vannak. Az eredmények kaotikusan változnak (az oldal negyedik ábrája). (A fenti ábrán pirossal rajzolt görbe pontos számított értékeket jelenít meg. A kék mező csak egy körülbelüli tartományt jelöl, amelyben az értékek elhelyezkednek. További kutatások során a kék tartományt is alaposan megvizsgálták. Grafikus megjelenítésű számítógépprogramokkal, ahogy a kisebb mérettartományok felé haladtak, végtelen sok üres sávot és elágazást találtak benne.)

Az ábrán látható kettéválásokat a Káosz-elmélet kutatói latin szóval bifurkációnak nevezik.

Nyitott szemmel járva a világban és a tudományokban, sok helyen fedezhetünk fel bifurkációkat, amelyek esetleg egy később kaotikussá változó folyamat előjelei lehetnek. A további cikkekben még számos példát láthatunk erre.

  Tudomány és Technika (test@t-es-t.hu)

<< Előző oldal    Vissza az oldal elejére    Következő oldal >>