Vissza a főoldalra Vissza a Tudományos érdekességek oldalra
|
A π
meghatározása a Leibniz-sorozat segítségével (2007.05.14.) |
Az alábbiakban egy érdekes felfedezést fogunk tenni, amelyet Leibniz már 1674-ben átélt a mértani sorozatok tanulmányozása közben.
A q = −x2 hányadosú mértani sorozat:
a1 = 1;
a2 = a1 · (−x2) = −x2;
a3 = a2 · (−x2) = −x2 · (−x2) = x4;
a4 = a3 · (−x2) = x4 · (−x2) = −x6;
·
·
an = an-1 · (−x2);
·
·
Vagyis: [1, −x2, x4, −x6, x8, −x10...].
Az első n elem összege a mértani sorozatok összegképlete alapján:
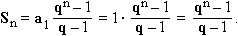
A végtelen mértani sorozat összege, ha | q | < 1:
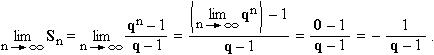
Behelyettesítve −x2-et (| x | < 1):
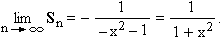
Tehát az összegre felírható (| x | < 1):
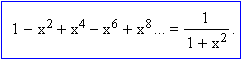
Mindkét oldalt integrálva:
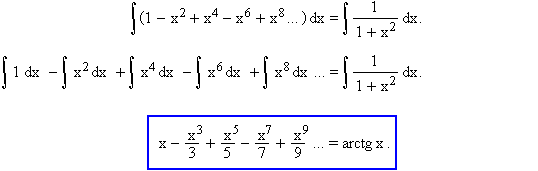
A tangens függvény inverzének grafikonja látható a következő ábrán.
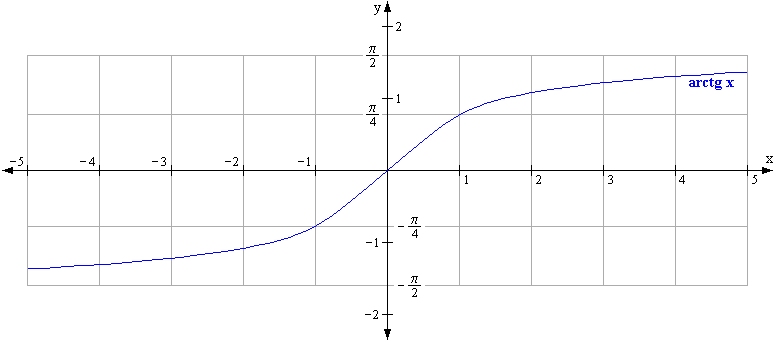
A grafikonból kiolvasható az arctg x függvény értéke az x = 1 helyen:
arctg (1) = π/4.
Az integrálás után kapott egyenletbe x = 1-et helyettesítve adódik az úgynevezett Leibniz-féle sorozat:
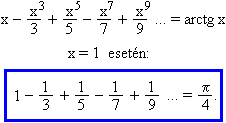
A π-t kifejezve:
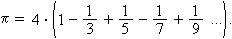
Ez egy viszonylag egyszerű képlet, így a számítások akár zsebszámológéppel is elvégezhetők. A következő táblázat a számítási eredményeket mutatja az első 40 részösszegig.
| A műveletek száma | A számítási eredmény |
| 1 | 4,0000000000 |
|---|---|
| 2 | 2,6666666666 |
| 3 | 3,4666666666 |
| 4 | 2,8952380952 |
| 5 | 3,3396825396 |
| 6 | 2,9760461760 |
| 7 | 3,2837384837 |
| 8 | 3,0170718170 |
| 9 | 3,2523659347 |
| 10 | 3,0418396189 |
| 11 | 3,2323158094 |
| 12 | 3,0584027659 |
| 13 | 3,2184027659 |
| 14 | 3,0702546177 |
| 15 | 3,2081856522 |
| 16 | 3,0791533941 |
| 17 | 3,2003655154 |
| 18 | 3,0860798011 |
| 19 | 3,1941879092 |
| 20 | 3,0916238066 |
| 21 | 3,1891847822 |
| 22 | 3,0961615264 |
| 23 | 3,1850504153 |
| 24 | 3,0999440323 |
| 25 | 3,1815766854 |
| 26 | 3,1031453128 |
| 27 | 3,1786170109 |
| 28 | 3,1058897382 |
| 29 | 3,1760651768 |
| 30 | 3,1082685666 |
| 31 | 3,1738423371 |
| 32 | 3,1103502736 |
| 33 | 3,1718887352 |
| 34 | 3,1121872426 |
| 35 | 3,1701582571 |
| 36 | 3,1138202290 |
| 37 | 3,1686147495 |
| 38 | 3,1152814162 |
| 39 | 3,1672294681 |
| 40 | 3,1165965567 |
A táblázatban a π-vel egyező számjegyek kék színnel vannak kiemelve. Jól látszik, hogy két oldalról közelítünk, hiszen a negatív tagok mindig a π alá, a pozitív tagok mindig a π fölé módosítják az összeget.
A következő táblázat néhány további számítási eredményt mutat be, amelyekhez már jelentős számítási teljesítmény szükséges.
| A műveletek száma | A számítási eredmény | A szükséges idő |
| 100 | 3,15149340107099058 | ~ 0,005 s |
| 1.000 | 3,14259165433954305 | ~ 0,05 s |
| 10.000 | 3,14169264359054322 | ~ 0,5 s |
| 100.000 | 3,14160265348979399 | ~ 5 s |
| 1.000.000 | 3,14159365358879319 | ~ 50 s |
| 10.000.000 | 3,14159275358978310 | ~ 500 s |
| 100.000.000 | 3,14159266358979398 | ~ 5000 s |
Megfigyelhető, hogy az összegbe bevont tagok számának (és ezzel a számítási időnek) a megtízszerezése körülbelül egy tizedesjegynyi pontosságjavulást okoz. Így kiszámíthatjuk, hogy mennyi ideig tart egy bizonyos pontosságú számítás. Például tíz tizedesjegynyi pontossághoz az alábbi számítógép- és program-konfigurációval kb. 1400 órás (58 napos) számításra volna szükség.
(A tesztelés egy Turbo Pascal 6.0 nyelven, DOS alá írt programmal lett végezve 350MHz-es órajelű Pentium II processzort tartalmazó gépen Windows ME operációs rendszer alatt. A DOS alá írt (16 bites) programok természetesen nem használják ki a fenti konfigurációban (32 bites) rejlő teljesítményt.) Itt a programlista és a futtatható program is letölthető.
Tudomány és Technika (test@t-es-t.hu)